Как найти площадь прямоугольника

Перед тем, как ответить на данный вопрос, необходимо вспомнить, какую фигуру называют прямоугольником и что такое площадь.

Что такое прямоугольник

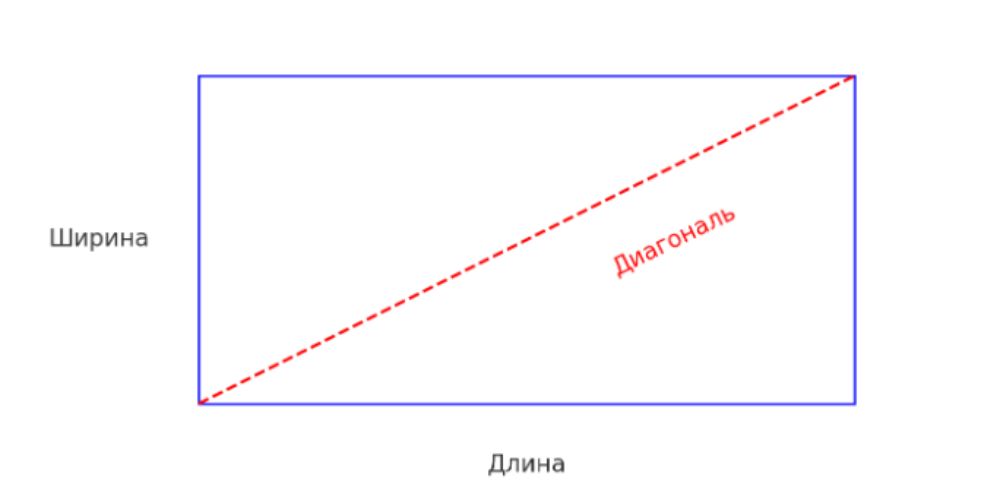
Прямоугольник — это четырёхугольник, у которого все четыре угла являются прямыми (то есть каждый угол равен 90 градусам).

Основные свойства прямоугольника

Противоположные стороны параллельны и равны

• Это означает, что если вы измерите любую пару противоположных сторон, то их длины будут одинаковыми.

Каждый угол прямоугольника равен 90 градусов, а сумма всех углов — 360 градусов

• Это определяющее свойство прямоугольника и отличает его от других четырехугольников.

Диагонали имеют одинаковую длину и делятся пополам в точке пересечения

• Хотя диагонали прямоугольника не равны сторонам и не образуют прямых углов с ними, они равны между собой по длине и точкой пересечения делятся на равные части.

Периметр и площадь

• Периметр прямоугольника вычисляется как сумма всех его сторон (2 длины + 2 ширины), а площадь находится путём умножения его длины на ширину.

Что такое площадь

Площадь — это мера, которая позволяет оценить размер двухмерной поверхности или фигуры в плоскости. Она выражается как количество единичных квадратов, которые полностью покрывают фигуру. Площадь измеряется в квадратных единицах, таких как квадратные метры (м²), квадратные сантиметры (см²), квадратные километры (км²) и так далее, в зависимости от размера измеряемой поверхности.

Понятие площади применяется ко многим геометрическим фигурам, включая квадраты, прямоугольники, треугольники, круги, многоугольники и даже более сложные формы. Для каждого типа фигуры существуют специфические формулы или методы вычисления площади, основанные на их геометрических свойствах.

Методы вычисления площади прямоугольника

Для вычисления площади прямоугольника используются несколько основных методов, которые меняются в зависимости от условий задачи и знания необходимых параметров фигуры.

• Стандартная формула. Это самый простой и наиболее часто используемый метод, в котором длина прямоугольника умножается на его ширину.

• Через диагонали и угол между ними (применяется в более общем случае для параллелограммов, включая прямоугольники). Для прямоугольника, учитывая, что диагонали равны и пересекаются под прямым углом, этот метод может быть использован с учётом, что sin (90) = 1

• Через диагональ и одну из известных сторон. В данном случае значения возводятся в квадрат, а также извлекается корень.

Когда известны длина и ширина прямоугольника

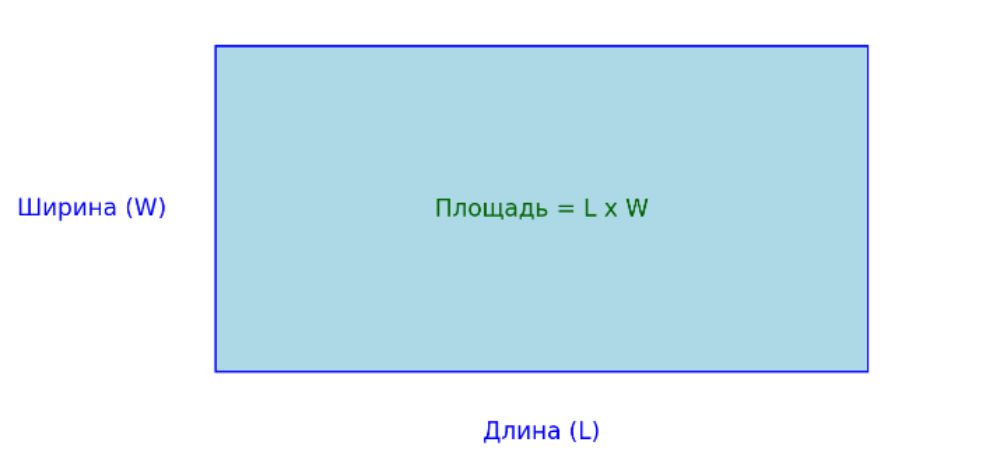
Это самый распространённый и прямой метод расчёта площади прямоугольника, который использует формулу:

• S (площадь) = длина (a) х ширина (b)

• Длина и ширина — это измерения двух смежных сторон прямоугольника. Этот метод подходит для всех прямоугольников, независимо от размеров сторон.

Если известна только диагональ прямоугольника

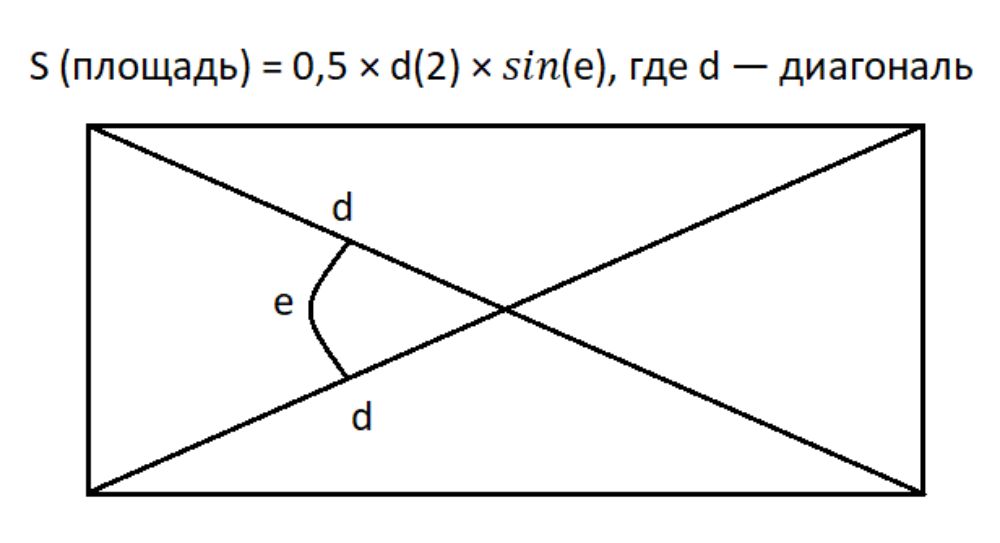
Для вычисления площади четырёхугольника без известных длины и ширины применима следующая методика: умножить половину произведения длин диагоналей на синус угла, образованного этими диагоналями.

• Формула: S = 0,5 х d(2) х sin(e), где d — диагональ

Диагональ представляет собой линейный отрезок, соединяющий две противолежащие стороны фигуры, присутствующий во всех многоугольниках с количеством вершин более трех. В случае прямоугольника диагонали идентичны по длине, так что знание одной диагонали и угла между диагоналями достаточно для подсчета площади.

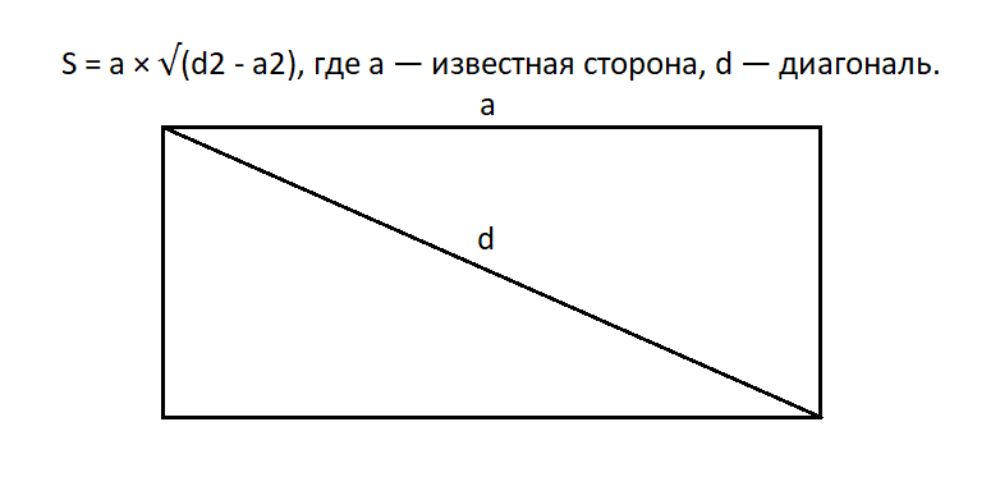
Если известна одна сторона и диагональ прямоугольника

Чтобы узнать площадь прямоугольника, зная только одну сторону и диагональ, можно найти их квадрат, затем вычесть из значения квадрата диагонали квадрат стороны, найти корень из полученного значения, и в конце умножить известную сторону на полученный результат.

Помните! Найти площадь прямоугольника не получится, если длина и ширина даны в разных единицах измерения. Все единицы измерения при вычислении должны быть приведены к одному значению (см2, м2, км2 и тд.)

Где используется площадь прямоугольника

Расчёт площади прямоугольника может быть полезен в различных профессиональных областях и бытовых ситуациях.

Строительство и архитектура

• Для планирования зданий, комнат, или распределения пространства на участке. Площадь помогает определить, сколько материала потребуется для полов, крыш, стен и т.д.

Дизайн интерьера

• Для определения размера ковров, напольных покрытий или для расчёта количества краски, необходимой для покраски стен.

Сельское хозяйство

• Для вычисления размера земельных участков, которые нужно засеять, и для расчета необходимого количества семян или удобрений.

Образование

• Как часть учебного процесса, для развития математических и аналитических навыков.

География и картография

• Для определения площади земельных и водных ресурсов, что может быть важно для планирования использования ресурсов, охраны природы и управления землепользованием.

Планирование мероприятий

• Для расчёта достаточного пространства для размещения гостей, столов, сцены и т.д. в залах для мероприятий или на открытых площадках.

Торговля и бизнес

• Для определения размера торговых площадей, складов, что важно для логистики, распределения товаров и управления запасами.

История открытия площади прямоугольника

История открытия формулы площади прямоугольника уходит корнями в глубокую древность, когда люди начали измерять землю и строить жилища, требуя точных расчётов размеров и площадей. Формула площади прямоугольника — произведение его длины на ширину — является одной из самых фундаментальных и интуитивно понятных геометрических формул, и её понимание было доступно уже древним цивилизациям.

Древний Египет

Одной из первых цивилизаций, начавших систематически использовать математику для измерения земель, был Древний Египет. Египтяне разработали сложную систему математики, которая включала в себя основы геометрии для разделения земель и решения практических задач, связанных со строительством. Например, они использовали верёвки с узлами для создания прямых углов при измерении границ земельных участков.

Древняя Месопотамия

Подобно египтянам, древние месопотамцы также имели развитую систему измерений и математики, которая позволяла им производить астрономические расчёты, планировать строительство и разделять землю. Вавилоняне, один из народов Месопотамии, оставили после себя глиняные таблички с математическими задачами и решениями, свидетельствующие о их продвинутых знаниях в области геометрии.

Древняя Греция

Формализация математики и геометрии, однако, достигла своего апогея в Древней Греции. Греческие математики, такие как Евклид, который жил около 300 года до нашей эры, систематизировали знания о геометрии в своих работах, наиболее известной из которых является «Начала». В этом труде Евклид изложил множество геометрических принципов и теорем, которые включают в себя и вычисление площадей. Хотя сама формула площади прямоугольника представляется собой более раннее открытие и не приписывается непосредственно Евклиду, его работы положили основу для систематического изучения геометрии, включая измерение площадей.

В итоге, формула площади прямоугольника, как и многие другие основы геометрии, является результатом накопления знаний многих древних цивилизаций, которые использовали эти принципы для решения практических задач. Эти знания были систематизированы и расширены в последующие века, формируя основу современной математики.

Статьи по теме

• Что такое хорда | 08.03.2024
• Что такое диаметр | 08.03.2024
• Что такое радиус | 08.02.2024
• Что такое натуральное число | 24.01.2024
• Что такое синус | 24.01.2024
• Что такое периметр | 20.01.2024
• Как найти процент от числа | 27.12.2023