Что такое хорда

Определение хорды

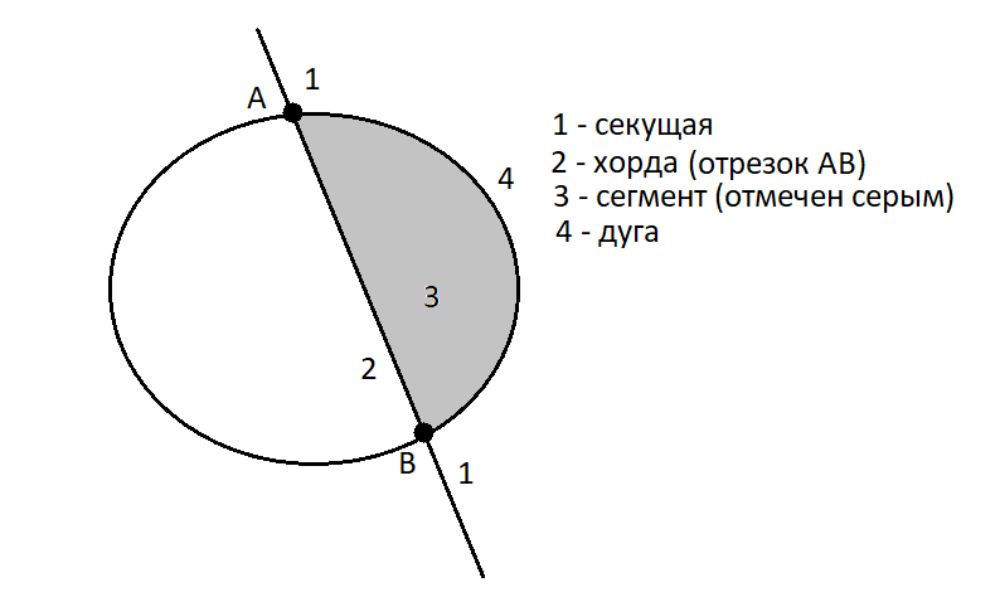
Хорда — это отрезок, соединяющий две точки на окружности или на кривой. Хорда располагается на секущей линии, которая представляет собой прямую, пересекающую кривую в двух или более местах.

Область, ограниченная кривой и ее хордой, называется сегментом, в то время как участок кривой между двумя конечными точками хорды именуется дугой. В контексте замкнутых кривых, таких как окружность или эллипс, хорда создает две дуги с одинаковыми конечными точками, расположенными по обе стороны от хорды.

Если хорда проходит через центр окружности, она называется диаметром, который является самой длинной возможной хордой в данной окружности.

Свойства хорд окружности

Хорды окружности обладают рядом интересных и важных свойств, которые находят применение в геометрии и связанных областях.

Хорда и центр окружности

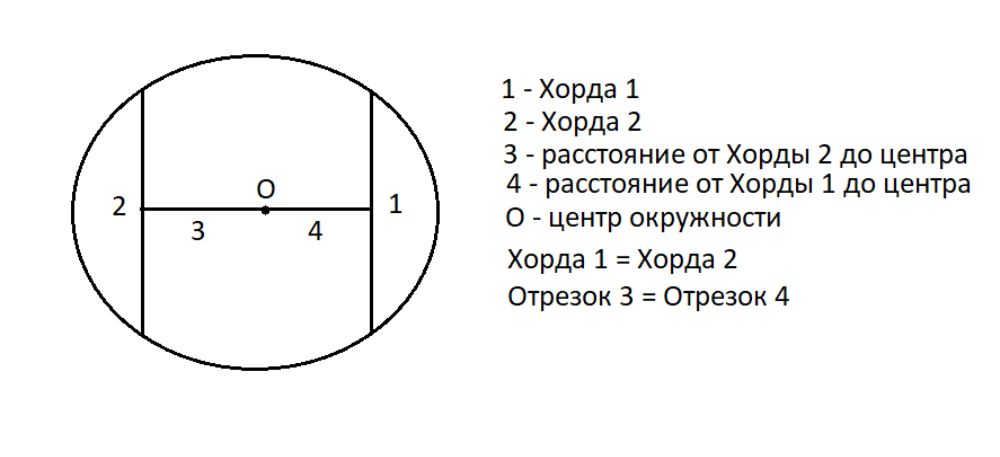
• Хорды, расположенные на одинаковом расстоянии от центра круга, имеют равную длину.

• При равенстве длин хорд, их расстояния до центра круга также совпадают.

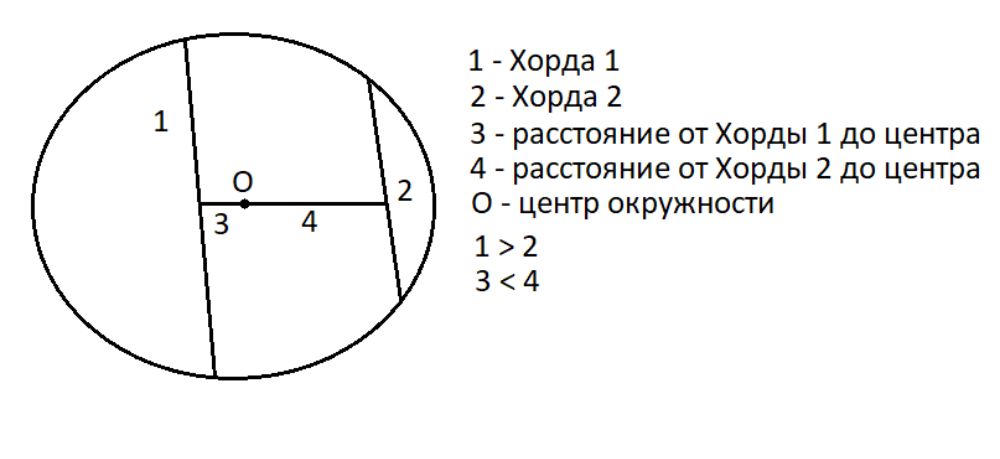
• Большая хорда находится ближе к центру круга, в то время как меньшая хорда расположена дальше от центра. Соответственно, меньшее расстояние от центра круга до хорды указывает на большую хорду, а большее расстояние — на меньшую хорду.

• Максимальная по длине хорда является диаметром круга. Хорда, проходящая через центр круга, определяется как диаметр.

• Хорда, отстоящая от центра круга на расстояние, равное его радиусу, представляет собой точку.

• Серединный перпендикуляр к любой хорде обязательно проходит через центр круга.

Хорда и диаметр

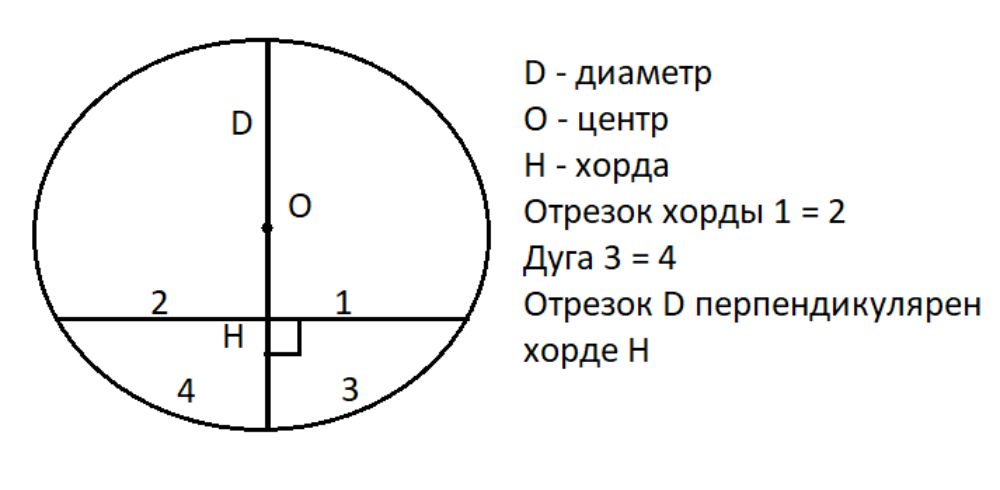
• Когда диаметр разделяет хорду, которая не совпадает с диаметром, на равные части, он также будет перпендикулярен этой хорде.

• В случае когда диаметр стоит перпендикулярно хорде, он разделит её на две равные части.

• Если диаметр разделяет на равные части хорду, не совпадающую с диаметром, он также равномерно разделяет дуги, которые эта хорда ограничивает.

• Когда диаметр делит дугу на равные части, он также делит на равные части хорду, формирующую эту дугу.

• Если диаметр находится под прямым углом к хорде, он разделяет на равные части дуги, образованные данной хордой.

Хорда и радиус

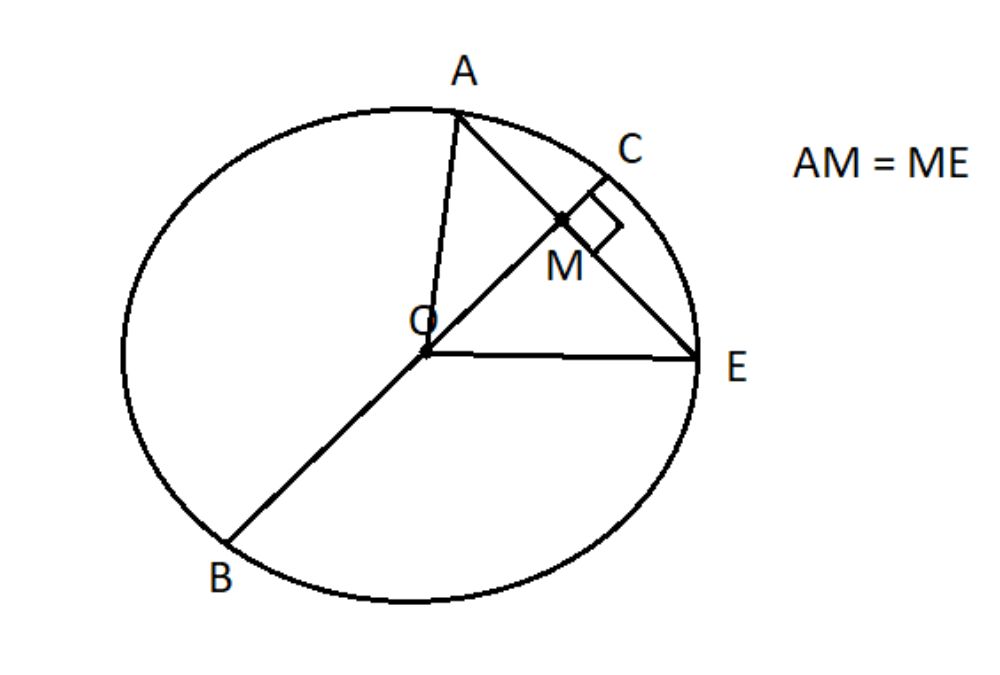
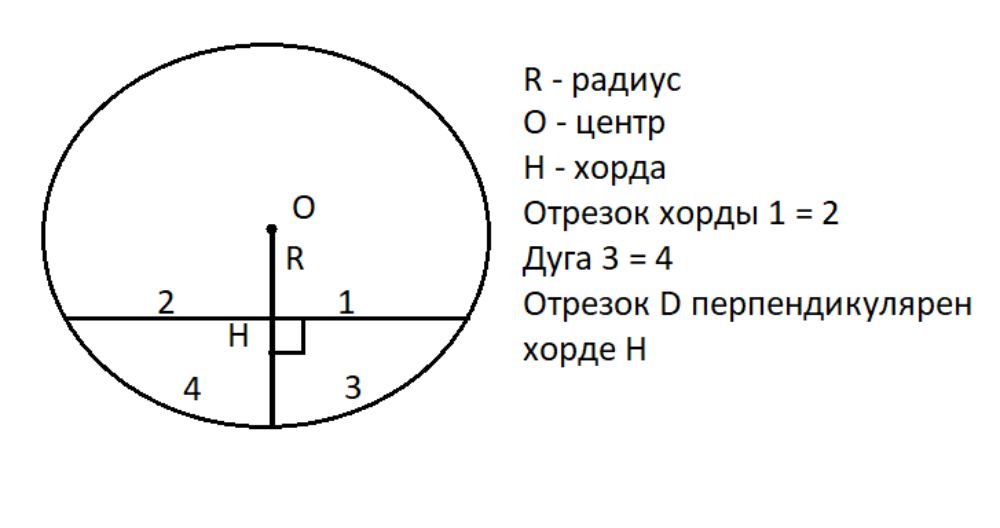
• Когда радиус разделяет на равные части хорду, которая не является диаметром, он оказывается перпендикулярным к этой хорде.

• Если радиус перпендикулярен хорде, он также разбивает её на две равные части.

• Разделение хорды на равные части радиусом, не совпадающим с диаметром, влечёт за собой деление на равные части и дуги, которую эта хорда ограничивает.

• Когда радиус делит дугу на равные части, он также разделяет на равные части хорду, образующую эту дугу.

• Радиус, находящийся под углом 90 градусов к хорде, разделяет на равные части дугу, формируемую хордой.

• Если радиус равномерно делит дугу, он будет перпендикулярен хорде, создающей эту дугу.

Хорда и углы

Вписанный угол

• Вписанные углы, имеющие общую основу на одной хорде и расположенные с одной стороны от неё, являются равными.

• Когда два вписанных угла основываются на одной хорде, но располагаются с противоположных сторон хорды, их сумма составляет 180 градусов.

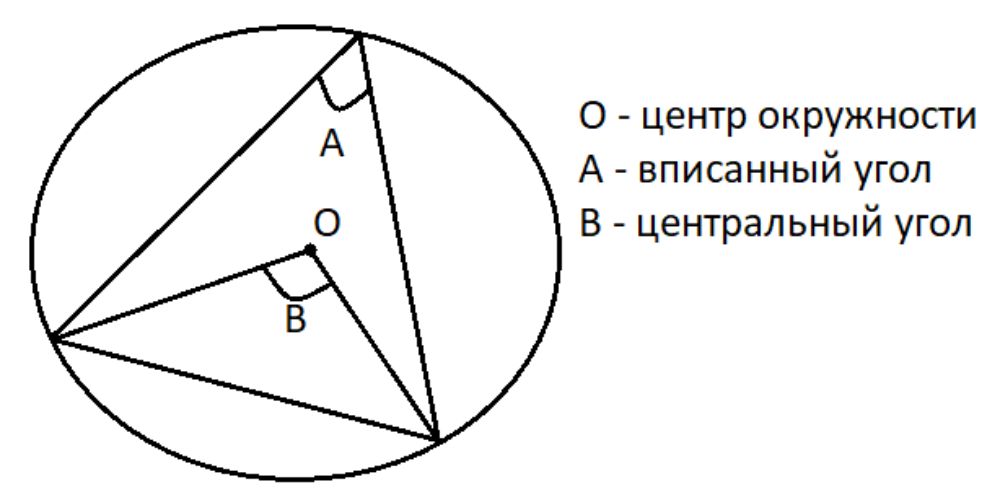
• В случае, когда вписанный и центральный углы основаны на одной хорде и находятся с той же стороны от неё, размер вписанного угла составляет половину размера центрального угла.

• Вписанный угол, основанный на диаметре окружности, всегда является прямым углом.

Центральный угол

• Хорды, формирующие одинаковые центральные углы, обладают одинаковой длиной.

• Когда хорды имеют равную длину, они образуют центральные углы одинаковой величины.

• Хорда большего размера соответствует большему центральному углу, в то время как хорда меньшего размера соответствует меньшему центральному углу.

• Следовательно, размер центрального угла увеличивается с увеличением длины хорды, которую он стягивает, и уменьшается с уменьшением длины хорды.

Хорда и дуга

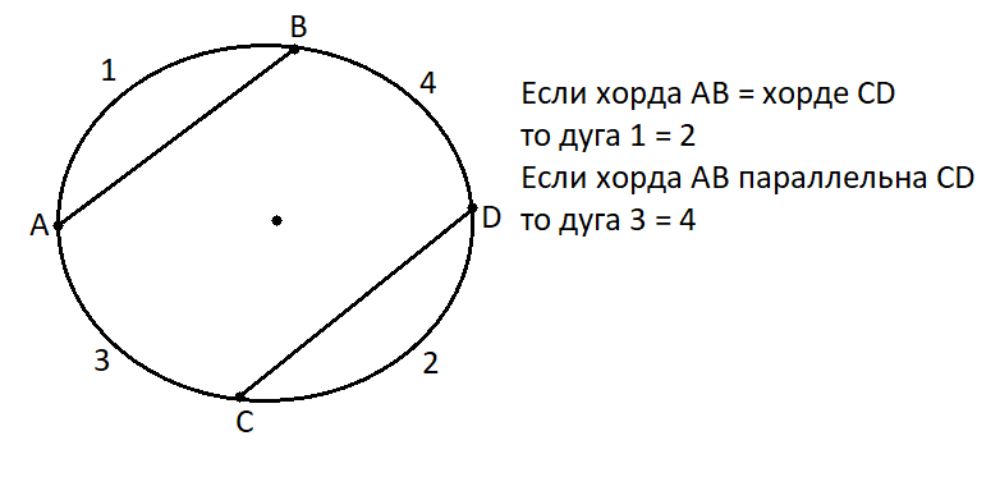
• Хорды, формирующие одинаковые дуги окружности, имеют одинаковую длину.

• Хорды одинаковой длины создают дуги одинаковой длины.

• Среди дуг, которые меньше половины окружности, длиннее хорда соответствует длиннее дуге, а короче хорда — короче дуге.

• Среди дуг, превышающих половину окружности, длиннее хорда сопровождается короче дугой, тогда как короче хорда — длиннее дугой.

• Хорда, образующая половину окружности, определяется как диаметр.

• Когда хорды расположены параллельно друг другу, дуги, ограниченные этими хордами, имеют равную длину, что не следует путать с дугами, которые непосредственно формируются хордами.

Иные свойства

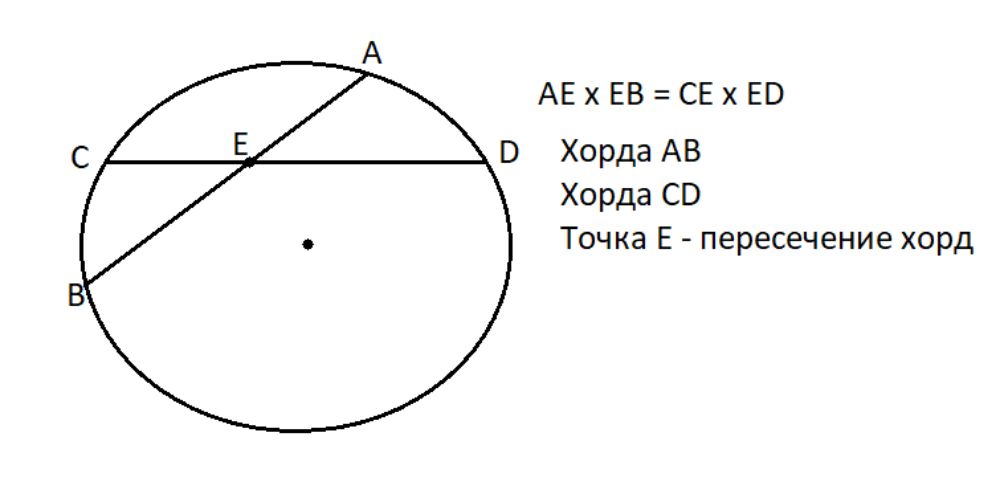
• При пересечении двух хорд AB и CD в точке Е получаются отрезки, произведение длин котороых у одной хорды равно такому же у другой хорды.

• При делении хорды пополам точкой, ее длина меньше длин проведенных через эту точку хорд.

Формулы, применяемые с хордами

Длина (L) хорды

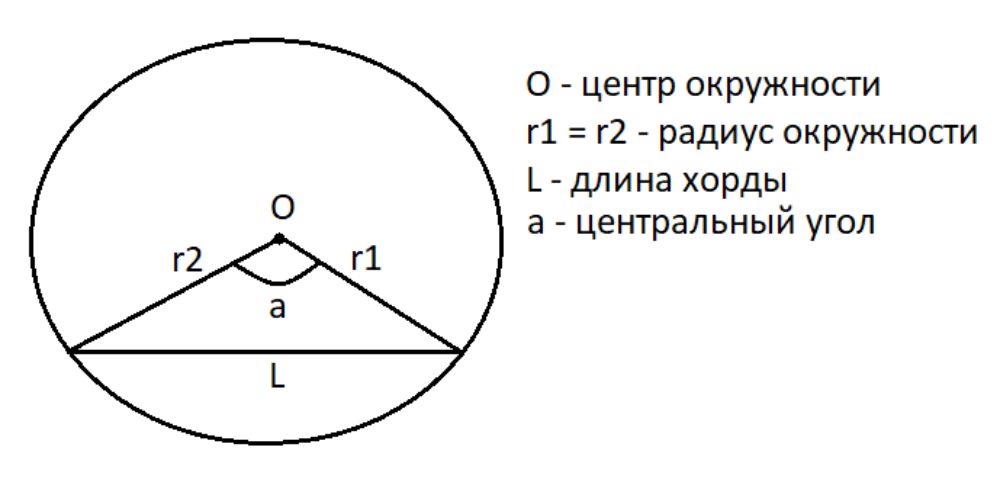
• L = 2 x r x sin a/2 = D x sin a/2

• Где r — радиус окружности, D — диаметр окружности, a — центральный угол, опирающийся на данную хорду

Формула с теоремой Пифагора

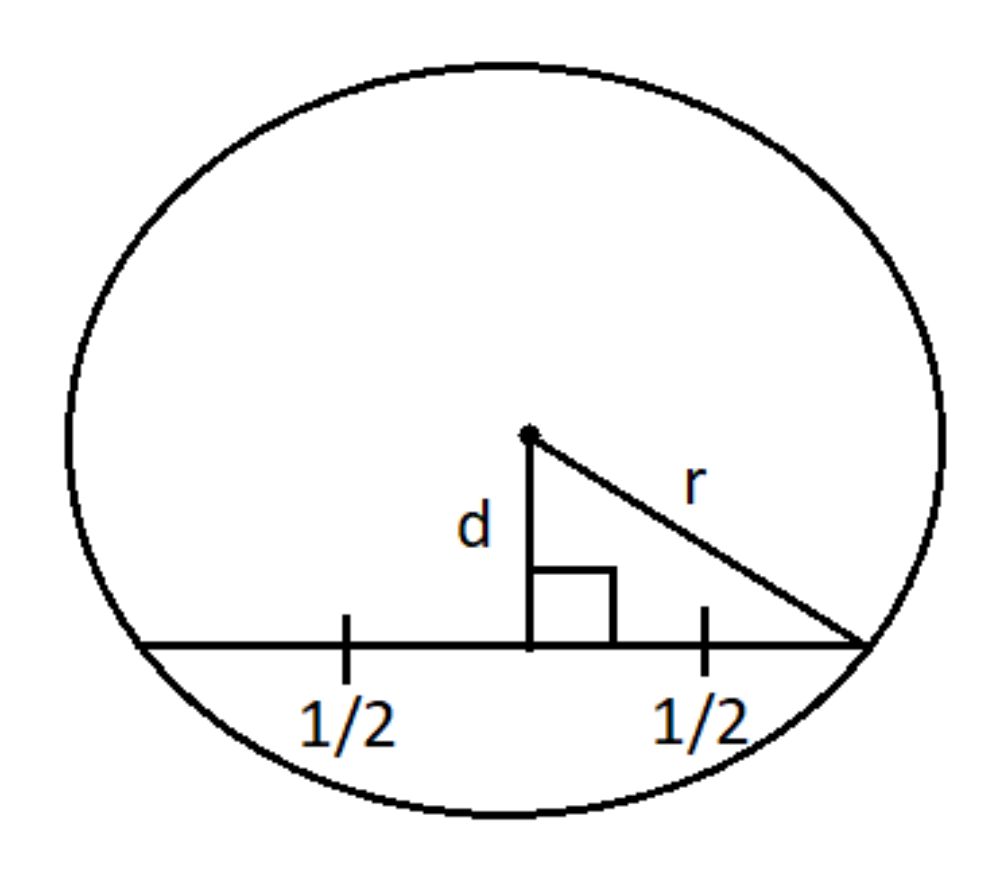
• (L/2)2 + d2 = r2

• Где L — длина хорды, r — радиус окружности, d — расстояние от центра окружности до хорды

В каких науках используется хорда

Хорды используются в множестве научных дисциплин, где они применяются для решения разнообразных теоретических и практических задач.

Математика

• В математике хорды играют центральную роль в геометрии, особенно в изучении свойств кругов и других криволинейных фигур. Хорды помогают в вычислении длин дуг, площадей секторов и сегментов, а также используются в доказательстве различных теорем.

Физика

• В физике хорды могут использоваться для моделирования траекторий, орбит и для анализа волновых явлений, где они помогают представить путь волн или частиц между двумя точками в пространстве.

Астрономия

• Астрономы используют хорды для измерения угловых размеров и расстояний до небесных тел. Хорды помогают в определении диаметров планет, звезд и других объектов, а также в расчете их орбитальных параметров.

Инженерия

• В инженерии хорды применяются при проектировании и анализе конструкций, включая мосты, арки, и другие архитектурные формы, где необходимо учитывать кривизну и нагрузку.

География и Картография

• В географии и картографии хорды используются для вычисления кратчайших расстояний между двумя точками на поверхности Земли, а также в процессе создания и интерпретации карт.

Компьютерная Графика

• В области компьютерной графики хорды применяются для генерации и рендеринга кривых и поверхностей. Они позволяют создавать плавные и реалистичные изображения криволинейных объектов.

Медицина

• В медицине хорды могут использоваться при анализе изображений, полученных с помощью МРТ или УЗИ, для измерения размеров и формы органов и тканей.

Эти примеры подчеркивают многообразие применений хорд в науке, демонстрируя их значимость в широком спектре дисциплин. Хорды служат важным инструментом в теоретических исследованиях и практических приложениях, помогая углубить наше понимание окружающего мира.

Историческая справка

История открытия и использования хорд в математике уходит корнями в древность и тесно связана с развитием геометрии и астрономии. Хотя точная дата или период, когда впервые было введено понятие хорды, не установлены, можно выделить несколько ключевых моментов и цивилизаций, внесших значительный вклад в развитие этого концепта.

Древний Египет и Вавилон

Древние цивилизации, такие как египтяне и вавилоняне, использовали ранние концепции, связанные с хордами, для астрономических наблюдений и строительства. Хотя они, возможно, и не формулировали понятие хорды в современном понимании, их работы по измерению углов и расстояний свидетельствуют о практическом применении этих идей.

Древняя Греция

Систематическое использование хорд началось в древнегреческой науке. Одним из первых, кто заложил основы тригонометрии, включая теорию хорд, был Гиппарх (2-й век до н.э.), который часто называют отцом тригонометрии. Гиппарх создал таблицу хорд, которая позволяла вычислять расстояние между двумя точками на окружности через угол, образованный этими точками и центром окружности. Такие таблицы хорд были предшественниками современных тригонометрических таблиц.

Александрийская школа

Великий александрийский математик Клавдий Птолемей (2-й век н.э.) расширил работу Гиппарха в своем труде «Алмагест», который оставался основным астрономическим справочником на протяжении многих веков. В «Алмагесте» Птолемей подробно описывает использование хорд для решения астрономических задач, включая предсказание затмений и движения планет. Это дало мощный толчок развитию астрономии и математики в последующие эпохи.

Индийская математика

Индийский математик Арьябхата (476 – 550 н.э.) далее развил теорию хорд, введя понятие синуса, который сегодня считается более удобным для тригонометрических расчетов, чем хорды. Его работы оказали большое влияние на развитие математики и астрономии в Индии и за её пределами.

Исламская математика

В период Золотого века исламской науки ученые, такие как Аль-Хорезми и Аль-Бируни, значительно расширили знания о хордах и тригонометрии, переведя и комментируя древнегреческие и индийские тексты, а также внося свои оригинальные вклады. Их работы способствовали передаче знаний о хордах и других математических концепциях в средневековую Европу.

Средневековье и Ренессанс в Европе

В средневековой Европе знания о хордах и тригонометрии продолжали развиваться, в значительной степени благодаря переводам исламских текстов. В эпоху Ренессанса интерес к астрономии и навигации стимулировал дальнейшие исследования в этой области, включая работу таких ученых, как Региомонтан и Иоганн Кеплер.

Таким образом, понятие хорды прошло долгий путь развития от древнегреческих астрономических расчётов до современной тригонометрии, играя ключевую роль в эволюции математики и науки в целом.

Статьи по теме

• Что такое диаметр | 08.03.2024
• Как найти площадь прямоугольника | 07.03.2024
• Что такое радиус | 08.02.2024
• Что такое натуральное число | 24.01.2024
• Что такое синус | 24.01.2024
• Что такое периметр | 20.01.2024
• Как найти процент от числа | 27.12.2023