Что такое диаметр

Определение и основные свойства

Диаметр — это прямая линия, проходящая через центр круга или сферы и соединяющая две точки на его поверхности. В математическом и геометрическом контексте диаметр является наибольшим расстоянием между двумя точками на окружности круга или поверхности сферы.

Диаметр окружности является хордой, проходящей через её центр; такая хорда имеет наибольшую длину.

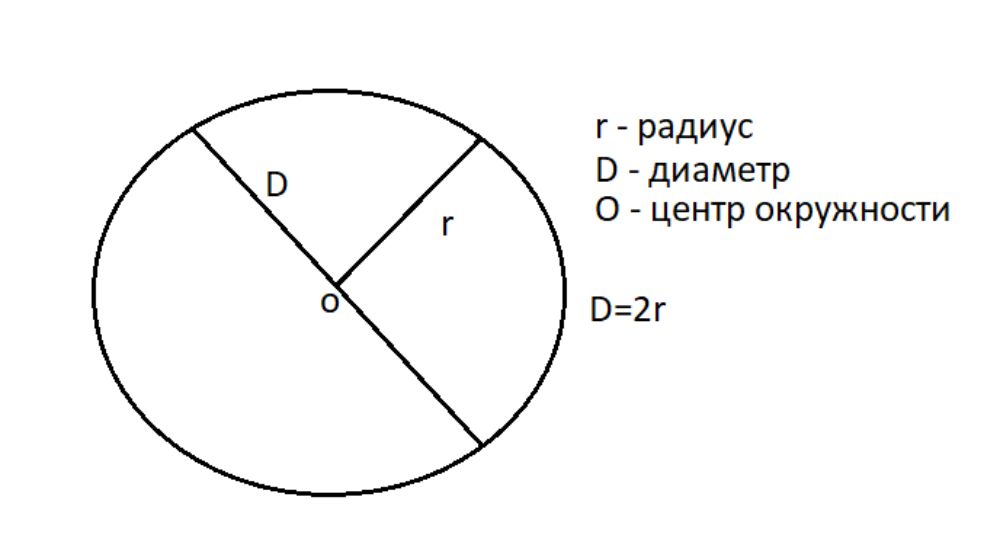
Диаметр в два раза больше радиуса, который представляет собой расстояние от центра круга или сферы до любой точки на его периферии.

Этимология (наука о происхождении слова) сообщает, что слово «диаметр» пришло в русский и другие языки из древнегреческого.
От др.гр. «διάμετρος» — «поперечник, диаметр», где «διά» — «через; раздельно» + «μετρέω» — «измеряю».

Термин «диаметр» также используется в переносном значении для описания ширины различных объектов, от труб до астрономических объектов, указывая на их максимальное поперечное измерение.

Интересный факт! Взяв любую окружность, в ней можно начертить бесконечное количество диаметров, так как она состоит из бесконечного числа точек, которые являются началом и концом отрезка — диаметра.

Как найти диаметр окружности

Диаметр окружности можно найти разными способами, в зависимости от того, какие исходные данные у вас есть.

Основные методы включают в себя использование:

• Радиуса окружности

• Длину окружности

• Площадь окружности

С помощью радиуса окружности

Если известен радиус окружности (r), то умножив это значение на 2, можно найти радиус диаметр (D) окружности.

С помощью длины окружности

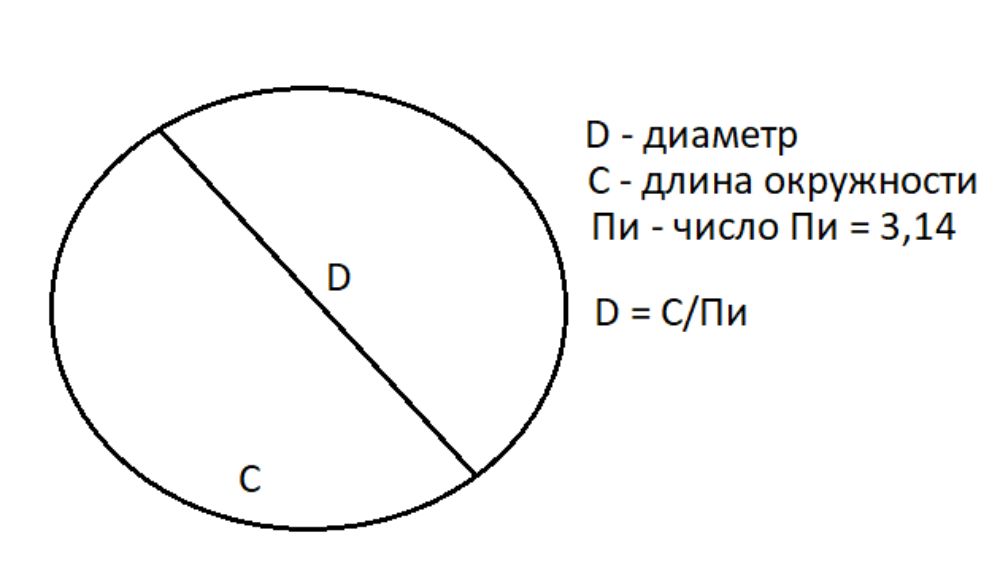
• Если известна длина окружности (C), диаметр (D) можно вычислить, используя формулу длины окружности и число Пи (3,14): C = Пи х D.

• Отсюда получается, что диаметр (D) = C / Пи

С помощью площади круга

• Если известна площадь круга (A), диаметр можно вычислить, исходя из формулы площади круга: A = Пи х r2

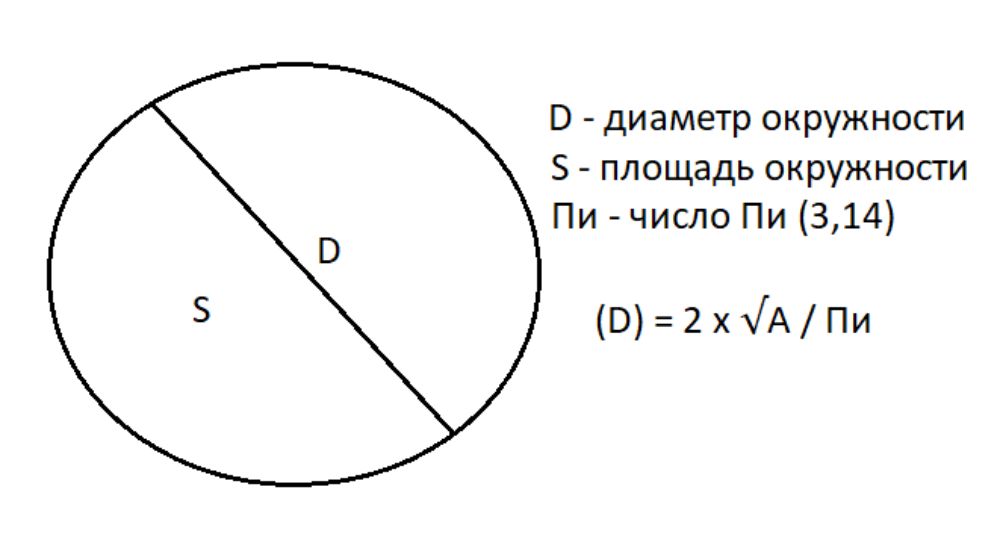
• Поскольку диаметр (D) = 2r, можно преобразовать формулу площади, чтобы выразить диаметр через площадь: радиус (r) = √A / Пи

• Тогда диаметр (D) = 2 x √A / Пи

Диаметр метрического пространства

Диаметр метрического пространства — это концепция, применяемая в математике, в частности в топологии и анализе, для описания наибольшего расстояния между любыми двумя точками данного подмножества метрического пространства.

Метрическое пространство — это множество, для элементов которого определена функция расстояния (метрика), удовлетворяющая определённым аксиомам. Эта метрика позволяет измерять расстояние между любыми двумя точками множества.

Суть уравнения

Пусть (M,d) — метрическое пространство, где M обозначает множество, а d — метрику на этом множестве, то есть функцию, которая каждой паре элементов x,y ∈ сопоставляет число d (x, y), представляющее собой расстояние между х и y. Тогда диаметр подмножества S ⊆ M определяется как:

• Диаметр (s) = sup {d(x,y)|x,y ∈ S}

Где sup обозначает супремум (верхнюю грань) множества расстояний между всеми возможными парами точек в S.

Значение

Диаметр метрического пространства даёт представление о размере пространства или его подмножества в смысле максимального расстояния между точками. Этот концепт широко используется в различных областях математики для анализа пространственных структур, исследования последовательностей и функций, а также в компьютерных науках, например, при анализе сетевых структур или алгоритмов кластеризации.

Примеры использования

• Анализ сходимости: Использование диаметра позволяет формализовать понятие сходимости последовательностей и функций в метрических пространствах.

• Топологическая компактность: В топологии диаметр используется для доказательства компактности множеств, что является ключевым понятием в анализе и геометрии.

• Кластеризация и анализ данных: В контексте кластеризации объектов по их признакам диаметр кластера может служить мерой внутренней согласованности группы.

Понимание диаметра метрического пространства и его свойств открывает двери для глубокого анализа пространственных структур и их поведения в самых разных математических и прикладных контекстах.

Где используется диаметр

Диаметр является фундаментальным понятием, которое находит применение в различных областях науки и техники, а также в бытовых ситуациях.

Вот некоторые из наук, где используется понятие диаметра:

Геометрия и математика

• В этих дисциплинах диаметр используется для описания свойств окружностей и кругов, включая вычисление периметра и площади, а также в задачах на построение и доказательство теорем.

Физика

• В физике диаметр применяется для описания размеров объектов, от атомов до звёзд. Он также используется в расчётах, связанных с динамикой вращательного движения, оптикой (например, диаметр линз и зеркал телескопов) и другими физическими явлениями.

Астрономия и космология

• В этих областях диаметр небесных тел, таких как планеты, звёзды, галактики, используется для оценки их размеров и сравнения между собой, что помогает учёным понять структуру и эволюцию Вселенной.

Инженерия и механика

• В технических науках диаметр используется для проектирования и изготовления множества объектов, от машинных деталей до строительных конструкций, обеспечивая их точность, надёжность и совместимость.

Медицина

• В медицине диаметр важен для измерения размеров органов, опухолей и других структур в теле человека с помощью различных диагностических инструментов, например, в радиологии и эндоскопии.

Биология

• В биологии диаметр используется для описания размеров клеток, тканей и организмов, а также для изучения их структур и функций на разных уровнях организации живой материи.

География и геология

• В этих областях диаметр применяется для оценки размеров географических и геологических объектов, например, кратеров, озёр, пещер и минералов.

Информационные технологии

• Хотя это может показаться неочевидным, но в IT диаметр используется в некоторых алгоритмах визуализации и моделирования, например, для определения границ объектов в компьютерном зрении и графике.

Таким образом, диаметр — это важный геометрический параметр, который находит широкое применение в различных областях человеческой деятельности.

Историческая справка

Концепция диаметра как меры размера объекта, особенно в контексте кругов и сфер, известна с древних времен и является одним из основных элементов в изучении геометрии. Однако, история открытия диаметра как математического понятия во многом сливается с развитием геометрии в целом и не приписывается какому-либо конкретному открытию или даже конкретному историческому периоду. Вместо этого, понимание диаметра развивалось параллельно с развитием математики как науки.

Древняя Греция

Важные вехи в понимании и использовании диаметра можно проследить в работах древнегреческих математиков. Евклид в своем фундаментальном труде «Начала» (около 300 г. до н.э.), систематически излагает основы геометрии, включая свойства кругов, хотя он прямо не определяет диаметр в современном понимании. Тем не менее, его работы легли в основу геометрического понимания форм и расстояний, включая идеи, связанные с диаметром.

Античность и Средневековье

В античные и средневековые времена знания о диаметре и его свойствах передавались и развивались через работы многих математиков и ученых, таких как Архимед, который сделал значительный вклад в изучение свойств круга, включая использование диаметра для определения площади круга и длины окружности.

Ренессанс и Новое Время

С наступлением Ренессанса и более поздних периодов в истории науки, математический анализ и геометрия продолжили развиваться, привнося более глубокое понимание свойств фигур и пространств, в том числе и концепций, связанных с диаметром. Работы таких ученых, как Рене Декарт, который ввел систему координат, позволили еще больше углубить изучение геометрических фигур и связанных с ними мер, включая диаметр.

Современность

В современной математике понятие диаметра было обобщено за пределы геометрии кругов и сфер и стало ключевым элементом в теории метрических пространств, играя важную роль в анализе и топологии.

История диаметра — это история математической мысли, отражающая развитие понимания пространства и форм. От древних геометров до современных математиков, изучение диаметра помогло углубить наше понимание мира и лежит в основе множества технологических и научных достижений.

Заключение

В заключение, диаметр играет фундаментальную роль в мире геометрии и выходит далеко за её пределы, оказывая влияние на множество аспектов нашей жизни, от науки и техники до искусства и повседневного использования. Это не просто мера длины через окружность, но и ключ к пониманию свойств кругов и цилиндров, основа для расчёта периметра и площади, а также важный параметр в проектировании и изготовлении объектов.

Понимание диаметра позволяет нам не только лучше осмысливать формы и пространства вокруг нас, но и улучшать и оптимизировать процессы и продукты, которые мы создаём. От астрономических исследований до архитектурного дизайна, от спортивных мячей до медицинских инструментов — диаметр является универсальным инструментом измерения, обладающим множеством применений.

Таким образом, понятие диаметра остаётся неотъемлемой частью нашего понимания мира, демонстрируя, как простая математическая концепция может обладать глубоким и многообразным значением.

Статьи по теме

• Что такое хорда | 08.03.2024
• Как найти площадь прямоугольника | 07.03.2024
• Что такое радиус | 08.02.2024
• Что такое натуральное число | 24.01.2024
• Что такое синус | 24.01.2024
• Что такое периметр | 20.01.2024
• Как найти процент от числа | 27.12.2023