Суббота, 20 января 2024 / Published in Справочник

Что такое периметр

Узнайте, что такое периметр — ключевая геометрическая концепция, определяющая длину границ фигур. Эта статья освещает основы периметра, методы его вычисления для разных форм и его практическое применение в повседневной жизни и науке.

Периметр – это длина контура или границы геометрической(плоской) фигуры. Другими словами, периметр – это сумма длин всех сторон фигуры. Он измеряется в единицах длины, таких как метры, сантиметры, дюймы и т. д. Периметр простой фигуры, такой как прямоугольник или круг, может быть найден путем суммирования длин всех сторон или, в случае круга, путем использования формулы, зависящей от радиуса или диаметра. Рассмотрим разные аспекты периметра подробнее:

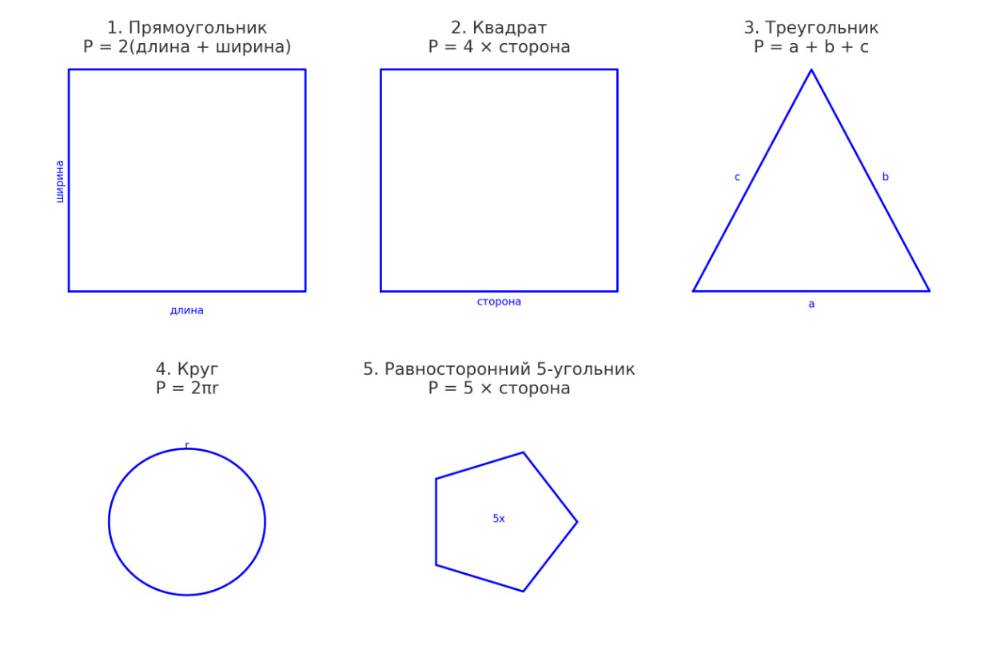
Cхема для вычисления периметра основных геометрических фигур:

Прямоугольник (фигура 1): Для вычисления периметра прямоугольника нужно сложить длины всех его сторон. Формула: P = 2 × (длина + ширина).
Квадрат (фигура 2): Квадрат — это частный случай прямоугольника, где все стороны равны. Формула: P = 4 х сторона, где «сторона» — это длина одной из сторон квадрата. Кроме того периметр квадрата можно вычислить через произведение длины его диагонали на два корня из двух, по формуле: P = d × 2√2
Треугольник (фигура 3): Периметр треугольника — это сумма длин всех его сторон. Формула: P = a + b + c, где a, b, и c — длины сторон треугольника.
Круг (фигура 4): Периметр круга, также известный как длина окружности, вычисляется по формуле P = 2πr, где r — радиус круга, а π=~3.14159. Обратите внимание, что это значение Пи является округлением, и для более точных расчетов может потребоваться использовать более длинное представление числа Пи.
Равносторонний многоугольника (фигура 5): Для равностороннего многоугольника (где все стороны равны) периметр равен P = n × длина_стороны, где n — количество сторон. То есть для фигуры в примере — равностороннего пятиугольника периметр вычисляется по формуле P = 5 × сторона.

Важно не путать периметр с площадью. Площадь относится к размеру поверхности фигуры, в то время как периметр только к длине её границы.

Области применения периметра

Периметр — ключевая концепция в геометрии, и он находит применение в различных областях, как в повседневной жизни, так и в научных и технических сферах.

Некоторые из основных областей использования периметра:

Архитектура и строительство: Периметр используется для определения длины границ земельных участков, оснований зданий, стен, ограждений и так далее. Это помогает в планировании конструкций и расчете материалов, необходимых для строительства.
Садоводство и ландшафтный дизайн: При проектировании садов, парков и других ландшафтных объектов периметр помогает определить длину границ, необходимых для ограждений, бордюров, тропинок и т. д.
Математика и образование: Периметр является фундаментальным понятием в математике, активно изучаемым в школьных курсах. В образовательной сфере задачи на нахождение периметра часто включают в себя проблемы, связанные с нахождением длин сторон фигур на основе заданных параметров. Он помогает учащимся развивать пространственное мышление и навыки решения задач.
Инженерия и проектирование: В различных областях инженерии, включая машиностроение, электротехнику и гражданское строительство, периметр используется для расчета границ и размеров компонентов.
Искусство и ремесла: В областях, требующих точного измерения и вырезания материалов, таких как ковка, столярное дело или ткачество, периметр помогает определить необходимые размеры.
Спорт и фитнес: Например, для определения длины беговых дорожек, границ спортивных площадок и бассейнов используется периметр.
Планирование и урбанистика: В градостроительстве периметр используется для планирования границ улиц, районов и зон различного назначения.
Аграрная сфера: Для определения границ полей, садов и других сельскохозяйственных угодий.

Это лишь некоторые примеры использования периметра, и их гораздо больше. В каждой из этих областей периметр помогает в точном определении границ и размеров, что является ключевым для эффективного планирования и реализации проектов.

История Формулы Периметра

История возникновения формулы периметра уходит корнями в древнюю геометрию и математику. Понятие периметра и методы его измерения развивались на протяжении многих столетий, начиная с древних цивилизаций, таких как Египет, Месопотамия, Индия и Греция.

Древний Египет и Месопотамия: Египтяне и вавилоняне (около 2000 г. до н. э.) были одними из первых, кто использовал концепцию периметра, особенно в землемерии и архитектуре. Для них периметр был практическим средством измерения земельных участков, особенно после ежегодных наводнений Нила, когда требовалось заново определять границы земельных владений.
Древняя Греция: Греческие математики, такие как Пифагор (около 570-495 гг. до н. э.) и Евклид (около 300 г. до н. э.), сделали значительный вклад в развитие геометрии. Евклид в своих работах, особенно в «Началах», систематизировал многие из известных математических знаний, включая концепции, связанные с периметром.
Индийская математика: В древней Индии математики также активно занимались геометрией. Работы, такие как «Сулба Сутры» (около 800-500 гг. до н. э.), содержат детальные инструкции по измерению и построению алтарей с использованием геометрических форм, что также предполагает понимание концепции периметра.
Древний Китай и другие цивилизации: В других древних культурах, включая Китай, также разрабатывались методы геометрических измерений, включая измерение периметра.

С развитием математики в эпоху Возрождения и в новое время, понятие периметра и связанные с ним формулы продолжали развиваться. Особенно это касается введения алгебраических методов в геометрию, что позволило более глубоко понять и обобщить концепции, связанные с измерением длин и площадей. Таким образом, формула периметра, как и многие другие математические концепции, является результатом векового накопления и обмена знаниями между различными культурами и цивилизациями.