Среда, 24 января 2024 / Published in Справочник

Что такое синус

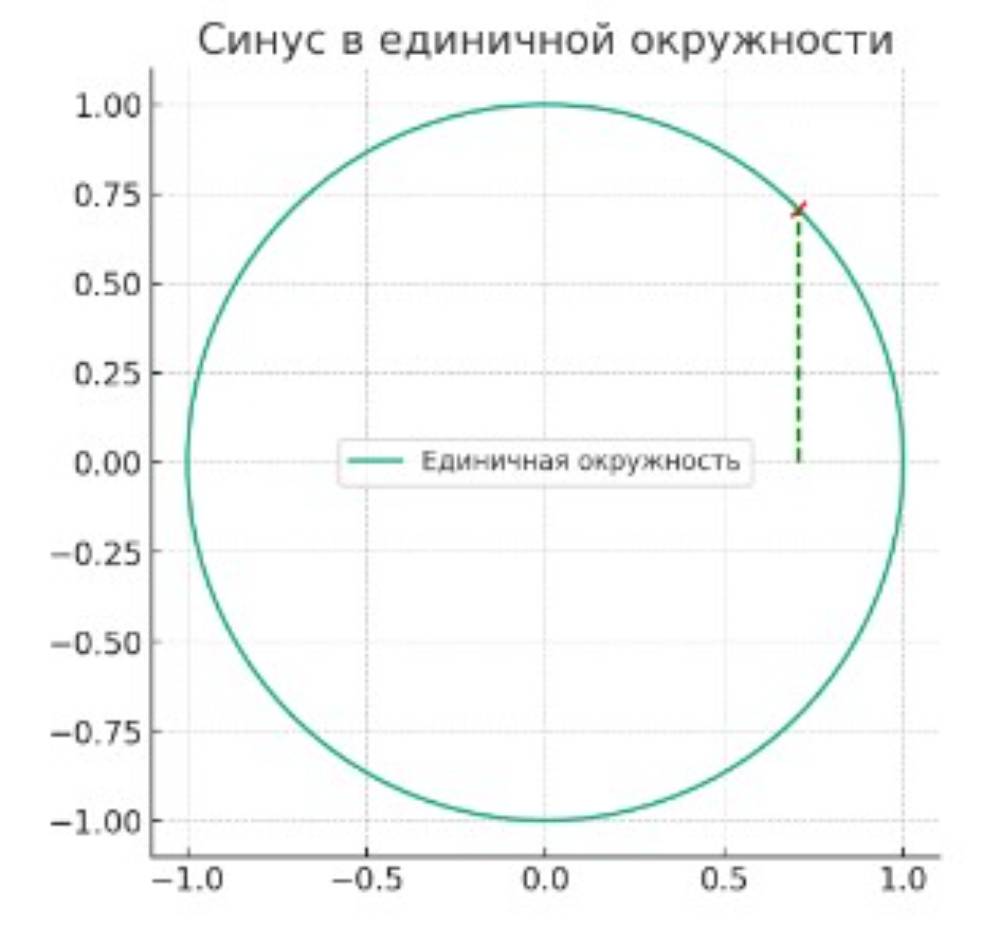
Синус – это тригонометрическая функция, которая играет важную роль в математике, особенно в тригонометрии и анализе. В самом общем виде, синус угла в единичной окружности – это длина отрезка, который проведен из точки пересечения окружности с осью X до проекции этой точки на ось Y.

Давайте рассмотрим синус более подробно

Определение Синуса в Единичной Окружности

Единичная окружность – это круг с радиусом 1, центр которого находится в начале координат в декартовой системе координат. Когда мы говорим о синусе угла, мы обычно рассматриваем угол, создаваемый радиусом окружности и положительной частью оси X.

Угол в радианах: Обычно углы измеряются в радианах при рассмотрении тригонометрических функций. Один полный оборот (360°) соответствует 2π радианам.
Синус угла θ: Это координата Y точки на единичной окружности, которая соответствует углу θ. sin(θ) = длина проекции точки на ось Y.

На рисунке, приведенном выше, показана единичная окружность, где синус угла (в данном случае 45° или π/4 радиан) представляет собой длину проекции точки на окружности (красная точка) на ось Y.

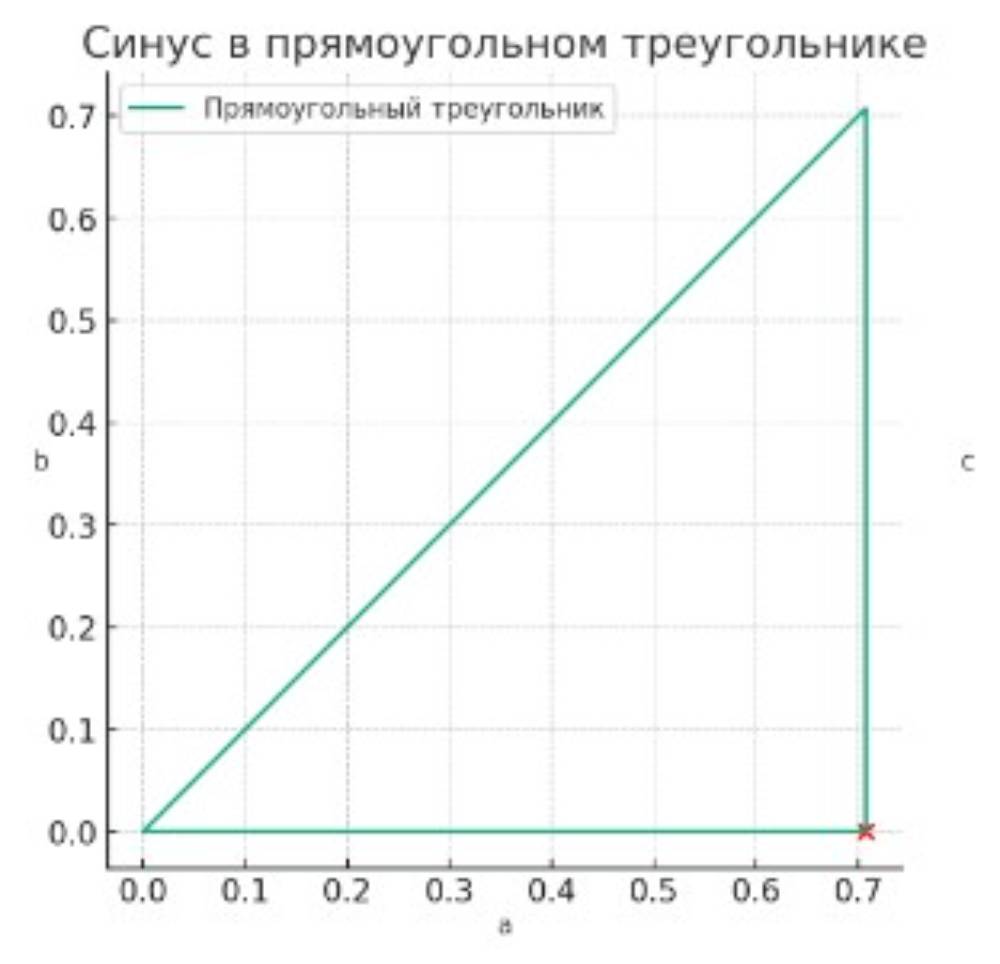
Синус в Прямоугольном Треугольнике

В прямоугольном треугольнике синус угла также определяется как отношение длины противолежащего катета к длине гипотенузы. Если у нас есть прямоугольный треугольник с углами A, B и C (где C – прямой угол), и длинами сторон a, b и c (где c – гипотенуза), то синус угла A будет равен sin(A) = (длина противолежащего катета) / (длина гипотенузы) = a / c.

На рисунке, приведенном выше, изображен прямоугольный треугольник, где синус угла равен отношению длины противолежащего катета (обозначенного как b) к длине гипотенузы (обозначенной как c).

Свойства и Значения

Диапазон Значений: Синус любого угла всегда лежит в пределах от -1 до 1. -1 ≤ sin(θ) ≤ 1
Периодичность: Синус – периодическая функция с периодом 2π радиан или 360°. Это значит, что sin(θ) = sin(θ + 2πk), где k — целое число.
Четность/Нечетность: Синус является нечетной функцией, то есть sin(-θ) = -sin(θ).

Применение

Анализ: Синус используется в различных аспектах математического анализа, включая интегралы и ряды Фурье.
Физика: Свойства синуса, такие как его периодичность и ограниченность значений, делают его незаменимым инструментом в анализе волновых явлений и гармонических колебаний в физике. Это не просто абстрактная математическая концепция; это ключ к пониманию фундаментальных природных процессов и явлений, от акустики до электромагнетизма.
Инженерия: В инженерных расчетах и проектировании синус играет важную роль, предоставляя необходимые инструменты для анализа сил и движений. Будь то в строительстве мостов, разработке аэродинамических форм транспортных средств или в электротехнике, применение синуса является ключевым элементом для успешного и безопасного дизайна.
Информатика: В компьютерной графике синус используется для создания волновых паттернов, анимаций и для моделирования движений.
Астрономия: Синус необходим для вычисления позиций небесных тел и траекторий орбит.
Музыка: Синусоидальные волны используются для описания музыкальных тонов и звуковых волн.
Медицина: В методах визуализации, таких как МРТ и УЗИ, используются принципы, основанные на синусоидальных волнах.
Экономика: Синусоидальные модели применяются для моделирования экономических циклов и тенденций.
Мореплавание: Синус применяется в морской навигации для определения курса и позиции судна.
Искусство и Дизайн: Синусоидальные кривые используются художниками и дизайнерами для создания эстетически приятных узоров и форм.

Синус – это ключевой элемент тригонометрии и широко используется в науке и инженерии. Его значение не только в том, что он предоставляет связь между углами и сторонами треугольника в тригонометрии, но и в его приложениях в различных научных и инженерных дисциплинах, от самых точных научных расчетов до творческого выражения в искусстве и дизайне. Синус – это не просто математическая функция, а мощный инструмент, который помогает нам понимать и интерпретировать явления вокруг нас.

История термина

Термин «синус» и его понятие являются одними из самых фундаментальных и влиятельных в мире математики. Эта концепция, прошедшая долгий путь развития и трансформации, является примером глубокого взаимодействия между различными культурами и эпохами, отражая эволюцию математической мысли и знаний. История синуса не только открывает уникальное окно в историю математики, но и демонстрирует, как идеи и знания могут пересекать границы и временные рамки, обогащая и трансформируя понимание человечества.

Происхождение в Индии

Концепция, ставшая основой для современного понимания синуса, была впервые разработана индийскими математиками. В частности, Арьябхата (476-550 н.э.) и Брахмагупта (598-668 н.э.) внесли значительный вклад в тригонометрию.

Термин «джйа», что означает «лук» или «полукруг», использовался для описания струны лука, то есть сегмента хорды, рассекающего круг. Это понятие похоже на современное понимание синуса. «Коджйа» (буквально «лук-со-стрелой») описывал то, что сегодня мы называем косинусом.

Развитие в Арабском Мире

Когда индийские тексты были переведены на арабский язык, термин «джйа» был переведен как «джиб», что в арабском языке означает «лук». Однако из-за схожести с арабским словом «джайб», означающим «карман» или «залив», произошло искажение перевода. Персидский математик и астроном Аль-Хорезми (ок. 780-850 н.э.) использовал термин «джайб» в своих трудах, что способствовало его распространению.

Переход в Европу

В 12 веке, когда арабские тексты начали переводиться на латинский, «джайб» был переведен как «sinus», что в латыни означает «залив» или «карман». Таким образом, арабский термин, изначально ошибочно ассоциированный с «карманом», был преобразован в латинский термин с аналогичным значением. После этого синус стал широко использоваться в европейской математике.

Современное Понимание

С развитием тригонометрии в 17-18 веках, концепция синуса продолжила развиваться, становясь все более похожей на современное понимание этого термина. Сегодня синус является фундаментальной концепцией в тригонометрии, необходимой в различных областях, от астрономии до инженерии.

История синуса является удивительной иллюстрацией того, как математическая концепция может путешествовать и эволюционировать через века и культуры, обогащаясь и преобразовываясь с каждым новым поколением ученых и математиков. От ее скромных корней в древней Индии, через адаптации в арабском мире и до окончательного принятия и расширения в Европе, синус стал неотъемлемой частью математического языка. Эта история служит напоминанием о том, как знания, развиваясь и передаваясь от одной цивилизации к другой, могут преобразовать наше понимание мира и способствовать научному прогрессу. Синус, в его современном виде, представляет собой не просто математическую функцию, а символ культурного и интеллектуального наследия человечества.